[最小全域木を求めるアルゴリズム] クラスカル法とプリム法の違い
最小全域木のまえに全域木(Spanning Tree)がどういうものなのかを確認しておきましょう。
Wikipediaによると
グラフ G(V,E) において T ⊆ E となる辺集合 T があるとき、グラフ S(V,T) が木(閉路を持たないグラフ)であるなら、 S(V,T) のことをグラフ G(V,E) の全域木であるとする。
参考 : https://ja.wikipedia.org/wiki/%E5%85%A8%E5%9F%9F%E6%9C%A8
もっとざっくりいうと、
頂点V,辺EをもつグラフGで、辺Eのなかのどれかの辺Tをつかい、それらの辺Tと頂点VからなるグラフS(V,T)が閉路、ループをもたない木ならば、グラフS(V,T)のことをグラフG(V,E)の全域木といいます、といったところでしょうか
で、全域木グラフS(V,T)の各辺に重みがある場合、それらの総和が最小で構成される全域木のことを最小全域木(Minimum Spanning Tree)といいます。
この最小全域木はネットワーク通信にとってとても重要なアルゴリズムで、ネットワークスイッチングハブがループを起こさずに効率的にデータを輸送するために利用されています。
クラスカル(kruskal)法とプリム(Prim’s)法
あるグラフがあたえられた場合、最小全域木を構成したいとします。では、どうやって最小全域木をみつければよいのでしょうか?そのためのアルゴリズムとしてクラスカル法とプリム法があります。
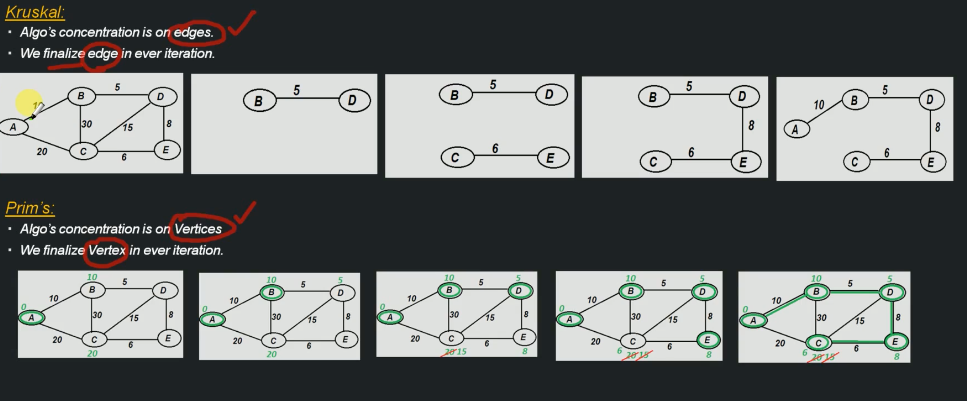
実装の違い
- クラスカル法 辺に着目
データ構造 : DisjointSet -
プリム法 頂点に着目
データ構造 : Priority Queue
計算量
-
クラスカル法 - 単純な貪欲法で計算量は O(Elog E)。
-
プリム法 - 貪欲法だが計算量はO(E+Vlog V)。辺の数が頂点に比べて十分大きいときはO(E) と見なせる。
辺の重みが均一の場合は幅優先探索で O(E) で求まる。
今回はここまでです。ではでは